The Maxwell velocity distribution
The applet on this page was originally created by me in 1997 thanks to a grant from the University of Arkansas Teaching Academy. It was updated in the summer of 2003 by Melinda Freeze thanks to an REU grant from the National Science Foundation
One of the ways in which Maxwell went beyond all the previous kinetic gas models was by calculating a velocity distribution for the gas particles. He reasoned that, if the molecules were constantly colliding with each other, they could not all have the same speeds: in two or more dimensions, even two identical particles, initially moving with the same speed, will in general undergo a speed change when they collide (even if the collision is elastic), as long as they do not meet head-on. Maxwell therefore expected the molecules to have, at any given instant, many different speeds, distributed, so to speak, around an average value which was probably close to the 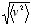 that Causius had calculated.
that Causius had calculated.
To obtain the mathematical form of this distribution of speeds, Maxwell searched for an equilibrium distribution, that is, a particular way to assign probabilities to all the possible velocities that would not change, overall, when a collision took place. What this meant was that, if two particles with velocities 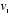 and
and 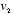 were to collide at such an angle that their final velocities became
were to collide at such an angle that their final velocities became 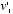 and
and 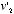 , the equilibrium velocity distribution should be one that assigned to the combination
, the equilibrium velocity distribution should be one that assigned to the combination 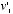 and
and 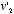 a probability equal to the one assigned to the initial combination
a probability equal to the one assigned to the initial combination 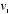 and
and 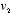 , times the probability that the collision should occur at that particular angle. Using Newton's laws of motion, and treating the molecules as perfectly rigid spheres, Maxwell could calculate
, times the probability that the collision should occur at that particular angle. Using Newton's laws of motion, and treating the molecules as perfectly rigid spheres, Maxwell could calculate 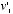 and
and 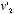 as functions of
as functions of 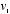 ,
, 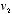 , and the collision angle, and thus write this self-consistency requirement in the form of a mathematical equation for the unknown function
, and the collision angle, and thus write this self-consistency requirement in the form of a mathematical equation for the unknown function 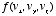 .
.
What is more, he could actually solve this equation; that is, he could show that there was a velocity distribution with the required properties. It turned out to be a Gaussian, a type of function whose ubiquitousness in probability theory was just beginning to be appreciated (so ubiquitous it is, in fact, that it eventually came to be called the "normal" probability distribution). From the distribution for the velocity, which is a three-dimensional vector, it is an easy matter to derive a corresponding distribution for the speed, which is a scalar quantity. In two dimensions, as for the "gas" of rigid disks whose behavior is calculated in the applet on this page, the formula is
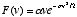
where 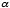 is a parameter related to the average speed:
is a parameter related to the average speed: 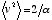 .
.
This equation is represented by the blue line in the small box on the right-hand side. The red bars in that box are a histogram of the particles' velocities at any given time. You can slow down the animation or pause it at any time. As you can see, all the particles start out with the same speed, but moving in random directions. Every time two particles collide, the computer applies Newton's equations to the collision to figure out what their new velocities should be. You'll notice that, after enough collisions, the distribution of velocities does indeed agree with Maxwell's theoretical predictions. You'll also notice that there are small fluctuations around the predicted value, which become proportionately smaller and smaller as the number of particles is increased.
In fact, Maxwell could not really show that the gas molecules would approach his equilibrium distribution, independently of the initial conditions. Because of its particular properties, though, it seems clear that if at some time the distribution of velocities is actually given by Maxwell's formula, it should stay like that, on average, for all later times, since further collisions would not change its shape. More intriguingly, however, it should also stay the same way even if at some time all the velocities of all the particles were reversed, since the distribution does not depend on the sign of the velocities. You can check that this is true by clicking "Stop" and then "Reverse" in the applet, after the distribution has the Maxwell shape. "Reverse" does, in fact, flip all the particles' velocities around and goes on calculating collisions from there.
There is, however, a serious conceptual difficulty with this result. The equations of mechanics are such that, if at any time you were to reverse all the velocities of the particles in a system, and then "let go," the whole system would retrace its steps, every collision's effects would be undone in order, and everything would return to its initial state. You can check that, in fact, the system in the applet does have this property for short enough times. (Try it! Run it until the number of collisions is of the order of the number of particles, then click "Stop," then "Reverse," and see what happens. It's even neater when you start with the "small grid" setting.)
But, you should ask, why only for short times? Where, and how is this microscopic irreversibility lost?
The answer will be on another page, since this one has run on too long already...
Forward to "Irreversibility"
Back to the introduction
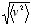 that Causius had calculated.
that Causius had calculated. 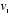 and
and 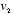 were to collide at such an angle that their final velocities became
were to collide at such an angle that their final velocities became 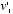 and
and 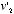 , the equilibrium velocity distribution should be one that assigned to the combination
, the equilibrium velocity distribution should be one that assigned to the combination 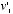 and
and 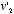 a probability equal to the one assigned to the initial combination
a probability equal to the one assigned to the initial combination 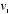 and
and 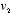 , times the probability that the collision should occur at that particular angle. Using Newton's laws of motion, and treating the molecules as perfectly rigid spheres, Maxwell could calculate
, times the probability that the collision should occur at that particular angle. Using Newton's laws of motion, and treating the molecules as perfectly rigid spheres, Maxwell could calculate 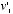 and
and 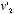 as functions of
as functions of 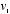 ,
, 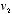 , and the collision angle, and thus write this self-consistency requirement in the form of a mathematical equation for the unknown function
, and the collision angle, and thus write this self-consistency requirement in the form of a mathematical equation for the unknown function 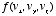 .
.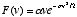
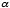 is a parameter related to the average speed:
is a parameter related to the average speed: 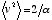 .
.