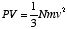
The kinetic theory of gases is called that to contrast it with earlier gas models, which involved essentially static atoms. The most popular such model, favored by the pioneering chemist John Dalton (around the year 1800), postulated the existence of point-like atoms surrounded by spherical "atmospheres" of caloric, the invisible fluid which was supposed to be responsible for most phenomena involving the exchange of heat. Caloric atmospheres supposedly repelled each other, and were also indefinitely expandable (for instance, as gas was pumped out of a container and became more rarefied); the atoms were thus always in contact, stacked up somewhat like billiard balls, and their mutual repulsion accounted for the gaseous pressure.
In contrast to this, a kinetic model of pressure had been developed by the Swiss mathematical physicist Bernoulli back in the 1730's, according to which the gas would consist of very small atoms in constant motion, and pressure would result from their collisions with the walls of the container. Bernoulli was able to prove the formula PV = (2/3)K.E., where P is the gas pressure, V its volume, and K.E. the total kinetic energy of the gas molecules. This result, however, was apparently ignored for a long time, and independently rediscovered in the first half of the 1800's by several people, including John Herapath, whose work, however, was rejected rather summarily, for years, by the British scientific establishment.
Since it was already known by the year 1800, after careful scales of temperature and thermometers had been devised, that the product PV for a gas was proportional to its temperature, the kinetic model's result suggested strongly that the temperature of a gas was a measure of the translational kinetic energy of its atoms. Such mechanical "explanations" of heat were not unheard of in those days, but they were generally rejected by most scientists, who tended to feel that the concept of caloric, in spite of its obvious difficulties (rendered all the more apparent after Count Rumford's experiments in the late 1700's), provided a better explanation of a number of heat exchange phenomena, especially those involving radiant heat.
Physicists as a whole did not become more open-minded towards the kinetic model until around 1850. By this time, the concept of energy was beginning to take shape, in essentially mechanical terms; the very careful experiments of James Prescott Joule, in particular, had established the possibility of accounting for a given rise in temperature entirely through an expenditure of mechanical energy. Yet even Joule's attempts to "push" the kinetic theory of gases were met with relative indifference.
The key impulse appears to have come from Rudolf Clausius, in Germany, in the years 1857-8. As others before him had done, he used the prediction PV = (2/3)K.E. to estimate the average speed of a gas molecule, by the following logic: let m be the mass of a gas atom (or molecule) and N the total number of molecules in the volume V. Then
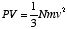
if all the molecules have the same speed v, or more generally
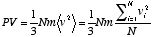
where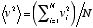 
is the average of the squares of the molecular velocities. Noting that mN is the total mass, M, of the gas, and that the density 
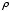is defined as 
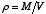, the above equation can be rewritten as
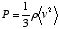
Here, the density and pressure of the gas are measurable quantities, and therefore the quantity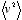 
(the average of the squares of the molecular velocities) can be computed. The result for the square root of that number was about 480 m/s for a typical air molecule at ordinary temperature and atmospheric pressure.
Clausius was a respected professor, and his interest in the kinetic model could not be as easily dismissed by the scientific establishment as that of his forerunners. His result for v was noticed, and an objection was immediately raised: if air molecules really travel at such fantastic speeds (larger than the speed of sound, but of the same order of magnitude), why is it that it takes some time, for instance, when one opens a flask of perfume in a corner of a room, for the scent to reach the opposite corner? At the speed of sound, the perfume molecules should spread throughout the room almost instantaneously.
The answer was, in fact, simple, but it prompted Causius to do a calculation that nobody had thought of before him, with momentuous consequences. What happens, he reasoned correctly, is that the gas molecules do not only collide with the walls of the container, but also with each other. Suddenly the, so far, wholly hypothetical molecules had acquired a finite size! The motion of any molecule through the gas is hindered by these continual collisions, which send it off flying randomly in all directions. Clausius introduced the concept of the "mean free path"--the average distance traveled by a molecule in between collisions--and proceeded to derive a formula for it: it should be, he concluded, inversely proportional to the product of the molecule's cross-sectional area and the overall gas density.
Since there was, at the time, no known way to estimate the size of a molecule independently, or to measure this hypothetical mean free path, Clausius's result might have been considered to be of academic interest only, but it was not so. Over in England, a young genius named James Clerk Maxwell read his paper and realized that here was a way to calculate a number of measurable properties of gases, and he plunged into the calculations with gusto. In a matter of months, he had derived expressions for a gas' viscosity, diffusivity, and heat conduction coefficient; obtained the distribution of speeds in a gas in thermal equilibrium; given a proof of Avogadro's conjecture regarding the number of molecules in equal volumes of different gases; and taken the first steps towards establishing the theorem of equipartition of energy. All of a sudden, statistical mechanics was born, and a full-fledged kinetic theory of gases had sprung into existence.